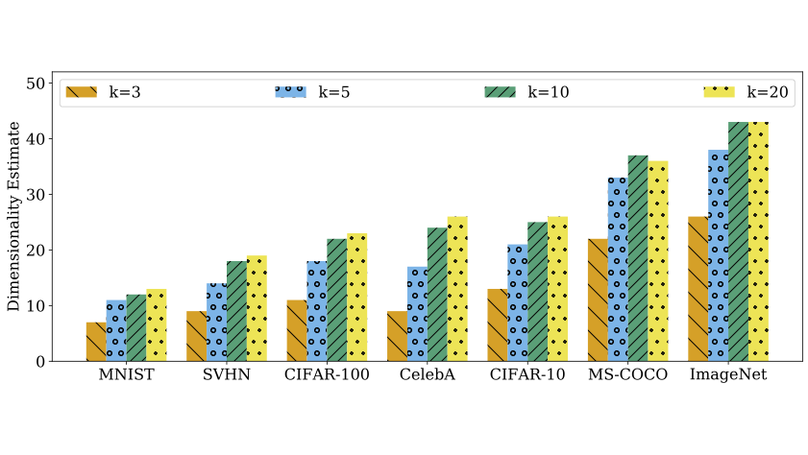
It is widely believed that natural image data exhibits low-dimensional structure despite the high dimensionality of conventional pixel representations. This idea underlies a common intuition for the remarkable success of deep learning in computer vision. In this work, we apply dimension estimation tools to popular datasets and investigate the role of low-dimensional structure in deep learning. We find that common natural image datasets indeed have very low intrinsic dimension relative to the high number of pixels in the images. Additionally, we find that low dimensional datasets are easier for neural networks to learn, and models solving these tasks generalize better from training to test data. Along the way, we develop a technique for validating our dimension estimation tools on synthetic data generated by GANs allowing us to actively manipulate the intrinsic dimension by controlling the image generation process.

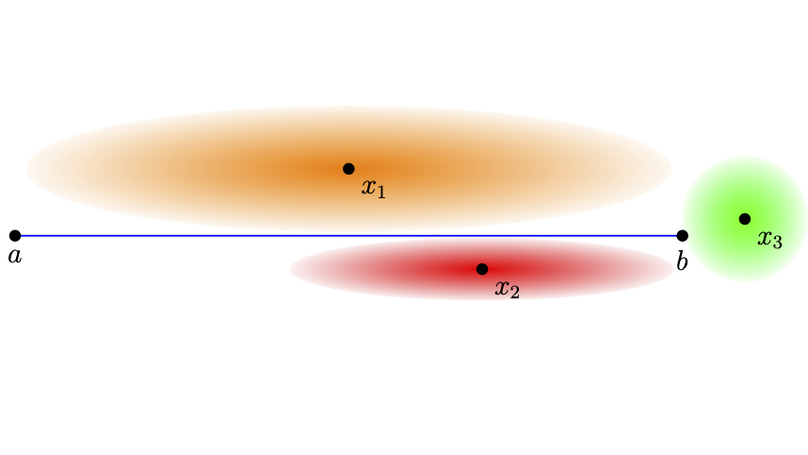
Approximate nearest-neighbor search is a fundamental algorithmic problem that continues to inspire study due its essential role in numerous contexts. In contrast to most prior work, which has focused on point sets, we consider nearest-neighbor queries against a set of line segments in $\mathbb{R}^d$, for constant dimension $d$. Given a set $S$ of $n$ disjoint line segments in $\mathbb{R}^d$ and an error parameter $\varepsilon > 0$, the objective is to build a data structure such that for any query point $q$, it is possible to return a line segment whose Euclidean distance from $q$ is at most $(1+\varepsilon)$ times the distance from $q$ to its nearest line segment. We present a data structure for this problem with storage $O((n^2/\varepsilon^d) \log (\Delta/\varepsilon))$ and query time $O(\log(\max(n,\Delta)/\varepsilon))$, where $\Delta$ is the spread of the set of segments $S$. Our approach is based on a covering of space by anisotropic elements, which align themselves according to the orientations of nearby segments.

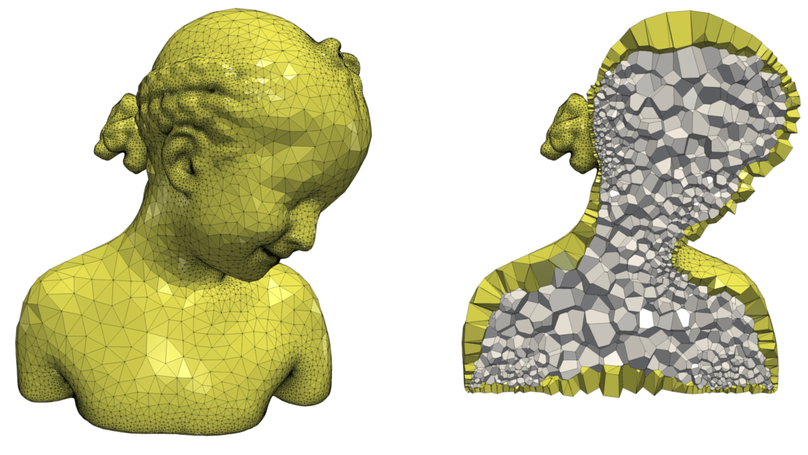
Polyhedral meshes are increasingly becoming an attractive option with particular advantages over traditional meshes for certain applications. What has been missing is a robust polyhedral meshing algorithm that can handle broad classes of domains exhibiting arbitrarily curved boundaries and sharp features. In addition, the power of primal-dual mesh pairs, exemplified by Voronoi-Delaunay meshes, has been recognized as an important ingredient in numerous formulations. The VoroCrust algorithm is the first provably correct algorithm for conforming polyhedral Voronoi meshing for non-convex and non-manifold domains with guarantees on the quality of both surface and volume elements. A robust refinement process estimates a suitable sizing field that enables the careful placement of Voronoi seeds across the surface, circumventing the need for clipping and avoiding its many drawbacks. The algorithm has the flexibility of filling the interior by either structured or random samples while preserving all sharp features in the output mesh. We demonstrate the capabilities of the algorithm on a variety of models and compare against state-of-the-art polyhedral meshing methods based on clipped Voronoi cells establishing the clear advantage of VoroCrust output.